The Critical Line – Volume 17, Christmas Edition

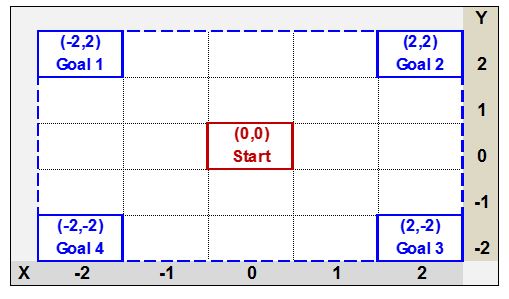
You start in the middle of a 5*5 grid at co-ordinates (0,0).  Each of the 4 corners of the grid is a Goal, and when you reach a goal your walk is over.  The goals and there co-ordinates are as follows:

• Goal 1 is at (-2,2)
• Goal 2 is at (2,2)
• Goal 3 is at (2,-2)
• Goal 4 is at (-2,-2)

Each time you take a step from the location (X,Y) you move either Up, Down, Left or Right with the following probabilities:

• P(Up) = 0.25 – 0.03*Y
• P(Down) = 0.30 + 0.05*Y
• P(Left) = 0.30 + 0.02*X – 0.02*Y
• P(Right) = 0.15 – 0.02*X

So there is a small tendency to be drawn back towards the centre of the grid.

Finally, this is a magic grid where the top and bottom are connected, and the left and right sides are connected.  Being on the edge and moving “off” the edge will take you to the opposite edge.  So for example if you are at (0,2) and take a step up, you will move to (0,-2).  If you are at (2,1) and take a step right, you will move to (-2,1).

The challenge is to determine the following:

• For each of the four Goals, the probability of your walk terminating at that Goal
• The probability your walk will take more than 20 step
• The expected value of the number of step in your walk

The Critical Line Volume 16 Solution

An Arithmetic Progression For any number $$n$$ let $$D(n)$$ denote the sum of the digits of that number. For instance $$D(1234) = 1+2+3+4 = 10$$. Does there exist a strictly increasing arithmetic progression with $$1000$$ terms, $$a_1, a_2, a_3, \dots, a_{1000}$$ such that $$D(a_1), D(a_2), D(a_3), \dots, D(a_{1000})$$ is also a strictly increasing arithmetic progression?

Solution

The answer is yes! Below is the proof submitted by this month’s only correct entry and winner Andrew Parker.

The proof is by way of construction. The arithmetic progression is of the form $$t_n = a + (n-1)\cdot d$$ for $$n = 1, 2, 3, \dots, 1000$$ where

$$a = \sum_{k = 1}^{200} (1000 – 5k)\cdot 10^{4(k-1)}$$

$$d = \sum_{k = 1}^{200} 5k \cdot 10^{4(k-1)}$$

This arithmetic progression has the property that

$$ \begin{align*}  t_{n+1} &= \sum_{k = 1}^{200} (10^4 – 5(k-n)) \cdot 10^{4(k-1)} \\ &= 10^4\cdot \sum_{k = 0}^{199} (10^4 – 5(k-(n-1))))) \cdot 10^{4(k-1)} \\ &= 10^4 \left( t_n + (10^4 – 5(0-(n-1)))10^{-4} – (10^4 – 5(200 – (n-1)))10^{4\cdot 199}  \right ) \\ &= 10^4t_n + (10^4 + 5(n-1))) – 5(n-1)10^{800} \end{align}$$

Note that while $$ 1 \le n \le 1800$$, the last two expressions will have at most four non-zero digits and we can write

$$\begin{align*}

 D(t_{n+1}) &= D(10^4t_n) +  D(10^4 + 5(n-1))) – D(5(n-1)10^{800}) \\

&= D(t_n) + D(1000 + 5n-5) – D(5n-5) \\

&= D(t_n) + 1

\end{align}$$

And therefore the sequence $$\{ D(t_n) \}_{n=1}^{1000}$$ is also an arithmetic progression with common difference $$1$$.

CPD: Actuaries Institute Members can claim two CPD points for every hour of reading articles on Actuaries Digital.