The Critical Line – Volume 37

The Problem

A 3x3x3 cube is made up of 27 blocks, each representing a whole number from 1–9 inclusive (numbers can be repeated). See the cube below:

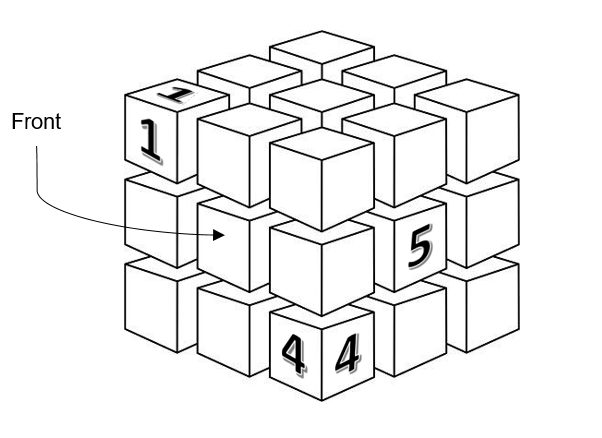
Your challenge is to solve for the unknown numbered blocks, given the following conditions:

1. Each slice of the cube must include a block of each number from 1–9 (inclusive). A slice is defined as a group of nine blocks in a 3x3x1 formation. Including internally, the cube has nine such slices.

2. The front slice of the cube (pictured including the 1 and 4), and the two parallel slices behind it, must have each row and each column sum to 15. This rule applies only to these three slices but doesn’t imply that other slices cannot hold the same principle.

Volume 36 solution

Congratulations to Kelvin Duong, who accurately completed the Vaccination Situation puzzle! In doing so, Kelvin earned himself a $50 book voucher.

Here is the solution

Part A

The ground floor is the most complex part to this problem and the trick is in the reception. There are many paths between reception and the stairs, but one must move once out of reception, then back into reception before proceeding. Here is how Kelvin went about it:

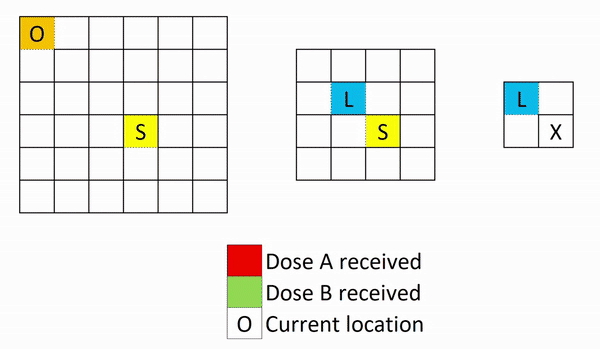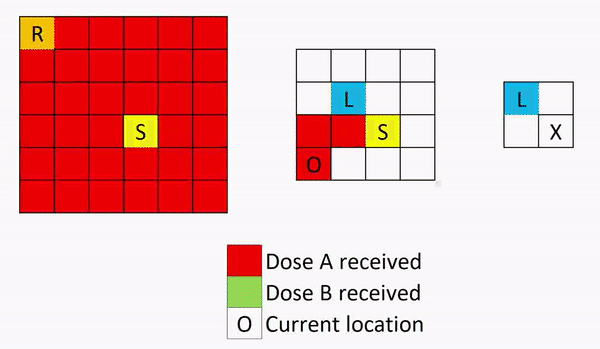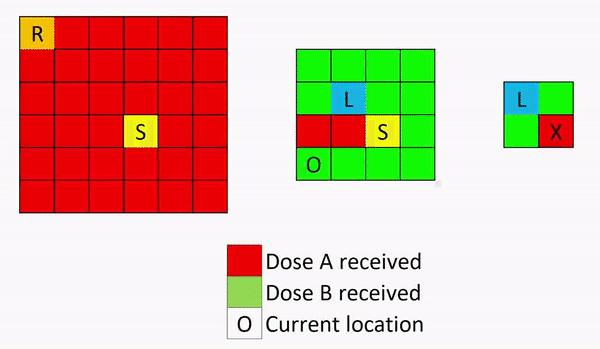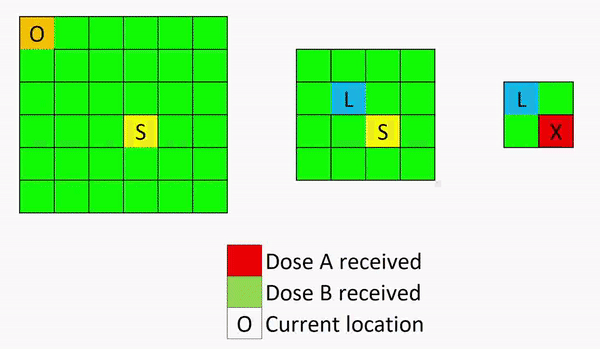
Once back on level 1, the reverse of the path shown in the first two images will complete the problem.

Part B

Under this new scenario, Part A becomes impossible. A simple logical explanation can prove this.

The ground floor can be thought of like a chessboard. Every new room entered can be seen as a single move from a black to a white square, or a white to a black square. The total number of squares here is even at 36. This means if one starts on a black square, it is inevitable to end on a white square, if each square is passed through exactly once. In fact, the same is true for any similar problem with sides of even numbers of squares.

The reception and stairs are on the same diagonal, which means they could be considered as both back squares, or both white squares. Therefore, it is impossible to begin in reception and end at the stairs without going back through reception to make the number of moves odd.

CPD: Actuaries Institute Members can claim two CPD points for every hour of reading articles on Actuaries Digital.