Virtual Summit Shorts: Neural networks in reserving – how and why are they worth considering?
Jenny Chen shares her learnings and thoughts from the Concurrent session ‘Neural Networks in Reserving: how and why are they worth considering?’ at the 2021 All-Actuaries Virtual Summit.
An accurate estimation of your insurance liability reserves could mean more efficient use of capital, more stable P&Ls, and a more robust financial outlook. One approach to achieve this is to use neural networks in reserving! In this article, I summarise the benefits, risks, variations and practical considerations of neural networks in reserving. In this article, I summarise the benefits, risks, variations and practical considerations of neural networks in reserving. Special thank you to Muhammed T. Al-Mudafer, Benjamin Avanzi, Greg Taylor, and Bernard Wong who did the study and produced the paper entitled “Stochastic loss reserving with mixture density neural networks”, where the contents, figures and results quoted here are extracted from.
What is a neural network?
Neural networks are a series of algorithms that recognise relationships between large sets of data by mimicking the operations of a human brain. The output of a neural network is a function of the input variables; they are connected by variable weightings and hidden layers. The output is determined by optimising the weight parameters.
What are the benefits of using neural networks in reserving?
- They can capture complex trends in the data;
- They have consistently outperformed the Chain Ladder on accuracy via back-testing;
- They are open to different types of data input, whether large, granular, or aggregate;
- They are efficient, being able to learn from multiple triangles simultaneously.
What are the risks and challenges? How to exploit and overcome?
Risk |
Potential Solution |
| Neural networks focus on the central estimate, rather than the whole distribution of outcomes, which is critical for risk management. | This can be solved by implementing a neural network that predicts the distribution, which is the Mixture Density Networks (MDNs). This method assumes that losses follow a Mixed Gaussian Distribution and can approximate various distributions with flexibility. A neural network is then set up to output the parameters of the distribution. |
| The process is a black box, so the results are hard to explain to stakeholders due to the low interpretability. | A hybrid approach can be used to improve interpretability. Methods such as ResMDN (GLM-MDN Hybrid Model) can be used, where a GLM is the backbone of the model, whilst a neural network is used for the residuals to pick up trends that are missed by GLM. Actuaries can apply their judgement to balance interpretability and modelling power of the method. |
| There is a lack of predictability for how the model will perform in the future when extrapolating data. There is also risk of over-fitting. |
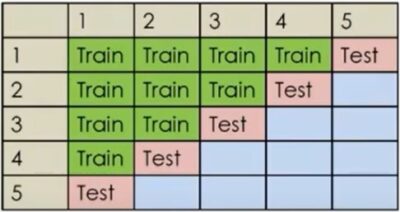
The model can be designed to incorporate actuarial judgement and set up restrictions on the estimation. This ensures reasonable projections. The data is split into a training set and a testing set based on time order. As the graph below demonstrates, testing set is the latest diagonal of the triangle. The model is optimised by assessing the accuracy of the projection going forward, this ensures the predictability of the model.
|
| It requires a lot of data. | It is tested that the approach performs well with a 40×40 triangle. |
How is the performance of MDN?
In the section below, I summarise the results of a Mixture Density Network that the presenters used on a reserving analysis.
Testing Data:
The data used includes 10 triangles of CTP long tail claims of real data from AUSI and 50 triangles simulated for each of the four different environments. The four environments include simple short tail claims, changing claim settlement processes, inflation shocks, and complex long tail claims. The variety of 210 triangles ensured the model is tested in a variety of situations.
Results:
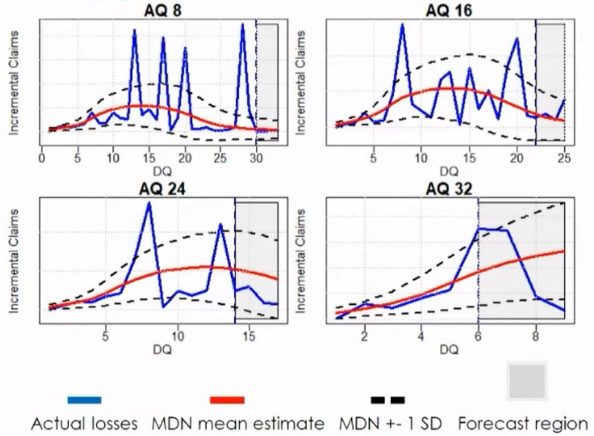
The top chart shows that the forecast (red line) is smooth and robust, even with volatile claims (blue line). To compare mean estimates, the Root Mean Squared Error of MDN is more than 15% lower than that of Chain Ladder.
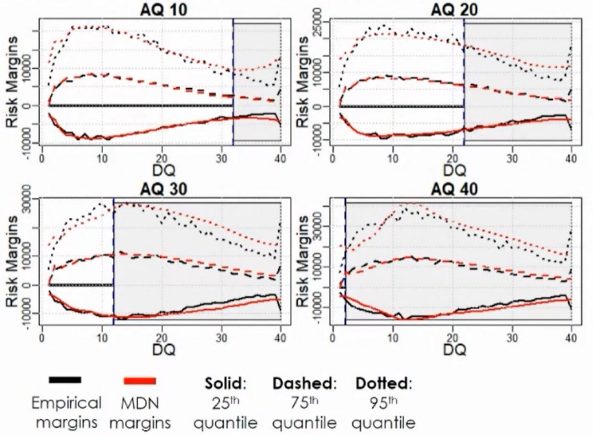
The bottom chart compares the empirical and MDN risk margins at various quantiles. This demonstrated that the MDN can capture the distribution of incremental claims. To compare distributional accuracy, the Log-Likelihood of MDN is consistently higher than that of the stochastic chain ladder. This means that the MDN method can also be used effectively for risk margin and capital management.
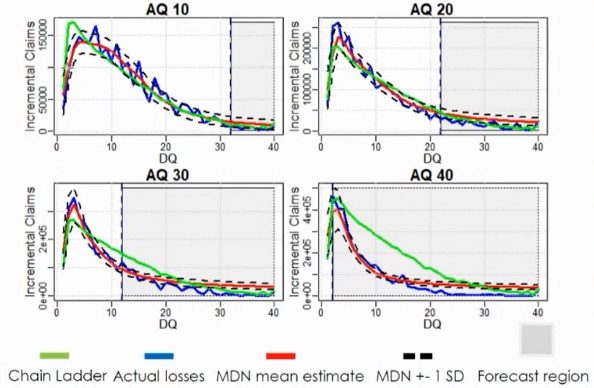
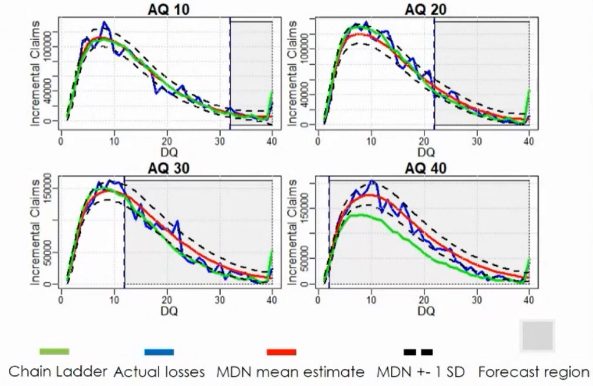
The top side chart displays the result when claims settlement speeds up. The MDN captures trends accurately, but the Chain Ladder method failed to do so.
The bottom chart shows that the MDN outperforms Chain Ladder in capturing inflation. The main reason is the Chain Ladder assumes trends develop homogenously, whilst MDN captures specific trends.
What are some future potentials of neural networks in reserving?
Besides fitting different mixture distributions to capture more trends, what’s more exciting is the idea of creating a ‘reserving brain’. Neural networks can be set up to learn from multiple triangles simultaneously, to create a ‘reserving brain’ that can be used in the projection of any individual triangles. This ‘reserving brain’ may also be applied for the whole industry, with the support of APRA. For such a data thirsty algorithm, the more data (clean data) that we feed it, the more accurate and robust the outcome will be.
I would like to thank the presenters for sharing their insights into such an interesting innovation within the actuarial reserving field. One, which I hope to employ within my reserving work one day.
|
Read further Actuaries Digital coverage of the 2021 All-Actuaries Virtual Summit. |
CPD: Actuaries Institute Members can claim two CPD points for every hour of reading articles on Actuaries Digital.