The Critical Line – Volume 33

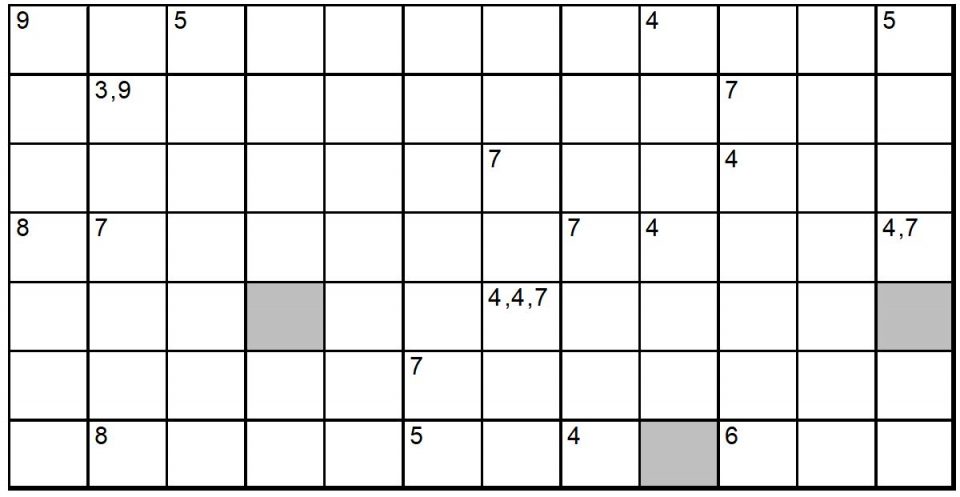
Your task is to fit all the given words from the table into the grid. Each word starts in a square corresponding to the length of the word, the second letter appears in the neighbouring square defined by the given direction. The third and remaining letters in the words must neighbour their preceding letter, but in any direction, left, right, up or down, one letter per square. The grey cells are blank.

Note that letters in the grid may be shared by multiple entries, though no letter may be reused within a single entry.

For your chance to win a $50 book voucher, send your solutions to ActuariesMag@actuaries.asn.au

Volume 32 Solution – by Dan Mayoh

Two correct answers were submitted to Part 1, by Tim Yip and Kelvin Duong.  Congratulations to both.  The winner of the book voucher is Tim Yip as he submitted his solution first.

Part 1:

After composing this question, I discovered it was essentially a rephrasing of a problem/result known as Bertrand’s Ballot Theorem.  The answer is (R-B)/(R+B).  So the probability depends only on the ratio of red to black cards.  For example, 7 Red and 3 Black has the same probability as 70 Red and 30 Black, i.e. 40%.

There a few ways to show this, and my favourite is Proof by Reflection.  It really is clever.  Have a look here.

Part 2:

The answer here is 16/693.  I solved this one by making a list of all 252,252 equally likely orderings that begin with 2 hearts (recognising that of the 16!/(6!*5!*5!) = 2,018,016 equally likely total orderings, 7/8 of these will not begin with 2 hearts and thus fail the condition, and do not need to be listed).  I then counted how many of those 252,252 orderings meet the condition (46,592), and simplified the fraction.  It’s not the neatest way, but it worked.  I am pleased to say though that a better way was submitted by Tim.  He used iteration, building up from an easy case of 2 hearts, 1 spade, and 0 clubs to arrive at the 46,592 value for the (6,5,5) case.

See Tim’s solutions here.

CPD: Actuaries Institute Members can claim two CPD points for every hour of reading articles on Actuaries Digital.