
Actuarial Cash Flow Model in Python
The actuarial cash flow model is an essential tool in any insurance company, helping the organisation predict and manage future financial outcomes of insurance portfolios.
In this article, we briefly describe the intuition behind insurance cash flow models and then get our hands dirty and build a simple life insurance model in Python ourselves, using a dedicated package.
Let’s start with some theoretical background.
How do cash flow models work?
In actuarial cash flow models, we are modelling expected, or average cash flows which will look very different to actual cash flows at a policy level. What does it mean? Let’s explain it with an example of a 5-year term life insurance.
At an individual policy level, the policyholder pays an annual premium (up until death), with a large payment on the event of death. An expected cash flow model takes the fractional likelihood of death each year (probability of claims times payout), giving a smooth picture of future payouts.
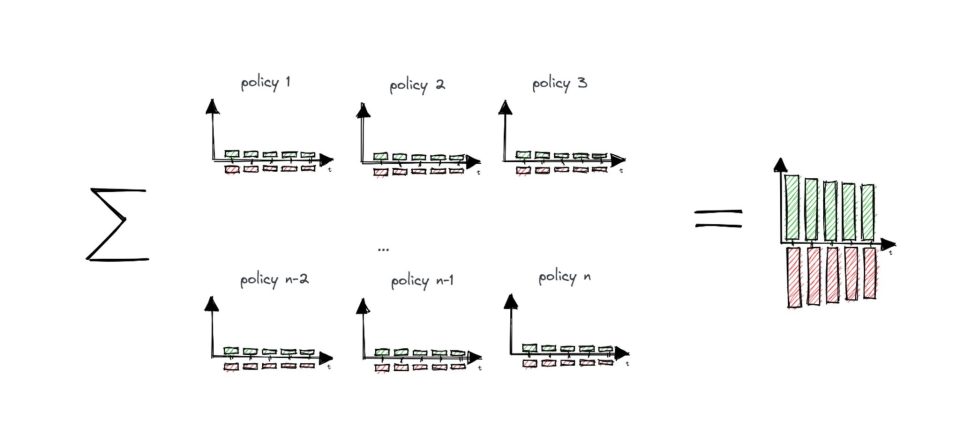
The model is not particularly useful at an individual level, since cash outflows will either be zero (no claim) or much larger than expected (in the case of a death). But by pooling policies across thousands of people, the law of averages will see actual cash flows approximate the sum of expected cash flows.
This is shown diagrammatically below – the first shows actual inflows (green) and outflows (red). The outflows in particular become much smoother on aggregation.
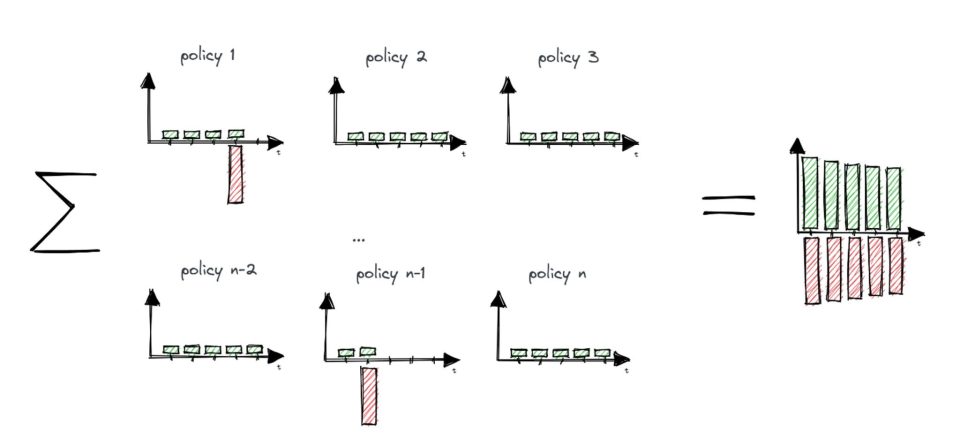
This overall distribution of cash flows can be modelled by combining expected flows:
Let’s build something!
With this picture of expected cash flows in mind, we can now jump in and build an actuarial cash flow model ourselves!
Actuaries develop cash flow models in various environments such as spreadsheets, commercial software or programming languages. In our example, we will use an open-source Python package cashflower. You can learn more about cashflower here – it is in active development, with an increasingly powerful set of features.
Now, let’s build a simple model to calculate a net single premium for a term life insurance. A net single premium is a premium that is paid once and which does not contain any risk loading. A n-year term life insurance provides a payment only if the insured dies within the n-year term of insurance commencing at issue.
Input
For simplicity, we will use constant monthly mortality and interest rate.
Source: https://gist.github.com/acturtle/a56c131de8391de15d351a89db1b1565
It’s a simplification because in the production actuarial cash flow models:
- mortality rates depend on the age and the sex of the policyholder,
- interest rates form a curve and vary for each future period.
It’s also usual that assumptions contain yearly data that must be converted into monthly rates within the model.
Now let’s create a model point set. We will populate it with only one model point. But a full model point set can contain thousands of model points.
Source: https://gist.github.com/acturtle/80aed62d2632fe752386d308a1171fd4
The policy data contains the sum assured and the term of the insurance. In our case, the term is expressed as the remaining term (starting from the valuation period) in months. So two years of the five-year term insurance have already passed. The policyholder still has three years of protection.
Model
The model contains the logic of the product. Our model will consist of the following model variables:
- survival rate;
- expected benefit; and
- net single premium.
Let’s define the formula for the survival rate:
Source: https://gist.github.com/acturtle/a3cd1b2596d2bde7b4a1511c69324d3f
The survival rate is the probability that the policyholder will survive from the beginning of the projection until a specific time in the future. It will help us to calculate the expected benefit:
Source: https://gist.github.com/acturtle/2119a4ecdf21caedb056d3a7b032972b
The person designated by the policyholder will receive the sum assured if the policyholder dies within the term. The expected benefit is then the sum assured multiplied by the probability that the policyholder survives until period t-1 and then dies in period t.
Source: https://gist.github.com/acturtle/3f48303618788cdb4ec69c368478f81a
The net single premium is the present value of the expected benefit payments. To calculate the present value, we use the discount rate calculated as 1/(1+INTEREST_RATE).
That’s it! We’ve calculated the net single premium as planned. Now let’s take a look at the results.
Result
The net single premium amounts to 9375.89 for our policyholder.
You can view the full model in the github repository here.
Exploring cashflower
Beyond the simple example we’ve built so far, the cashflower package offers a range of advanced features that make it a powerful tool for developing actuarial cash flow models. Let’s delve into some of these features to showcase the versatility and usefulness of the package.
Modelling liabilities together
Insurance companies often manage multiple insurance products simultaneously, each with its unique characteristics and cash flow patterns. The cashflower package allows you to model various liabilities together, which is a common scenario in real-world actuarial work. In our example, we only used one model point but in production models use thousands or more model points.
In cashflower, you can define as many model points as you want:
You can also read them from a file…
…or directly from a database:
Source: https://gist.github.com/acturtle/a423976c6d1690fc7bd78443ea47caac
If your model points are split across multiple files, simply declare multiple model point sets:
You can also manage the results in various ways. By default, cashflower saves results in a comma-separated values (csv) file, but you have the option to change this. You can save results to any location, use any file format, or directly insert them into a database The model’s settings allow you to adjust the projection and output horizon. For improved speed, you can activate multiprocessing, which evaluates the model across multiple cores simultaneously.
Power of open-source
The cashflower package is an open-source tool, freely accessible to all users. Positioned between spreadsheet functionality and commercial software, it offers a unique balance. While spreadsheets are user-friendly, they lack programming capabilities, unlike commercial software which tends to be expensive and restricted to corporate use.
The cashflower package is available on the Python Package Index (PyPI). The package can be installed using a single command:
By working within the Python environment, you can seamlessly integrate your project with other popular libraries, enhancing the capabilities of your modelling workflows.
The cashflower package democratizes actuarial modelling, fostering a community of developers, business professionals, and academic researchers. Open-source software relies on a community that collaborates to share practical knowledge, continuously improves the software and raises new ideas.
Are you interested in the development of actuarial cash flow models in Python? Learn more about the open-source cashflower package and join our community.
CPD: Actuaries Institute Members can claim two CPD points for every hour of reading articles on Actuaries Digital.






