The Critical Line – Volume 16

Warming Up

1. Let $$D(n)$$ denote the sum of the digits of the integer $$n$$. For instance $$D(1234) = 1+2+3+4 = 10$$. Find all integers $$n$$ such that $$n + D(n) + D(D(n)) = 2017$$

[reveal heading=”

%image% Click to reveal/hide solution

” id=”id1″]SOLUTION: 

Note that both $$n$$ and the sum of the digits of $$n$$ leave the same remainder when divided by $$3$$. That is $$n \equiv D(n) \text{mod} 3$$. This means $$n + D(n) + D(D(n)) \equiv 3n \equiv 0 \text{mod} 3$$, however $$2017 \equiv 1 \text{mod} 3$$ so there are no solutions!

[reveal]

2. Does there exist an arbitrarily long sequence of perfect powers (i.e. numbers of the form $$n^m$$ for some $$n,m \in \mathbb{Z}$$) that form an arithmetic progression?

[reveal heading=”

%image% Click to reveal/hide solution

” id=”id2″]SOLUTION: 

The answer is yes! We construct such a sequence using induction. The base case is clear because any sequence of two integers is an arithmetic progression. Now assume we have an arithmetic progression of length $$k$$ with a common difference of $$d$$

$$n_1^{m_1}, n_2^{m_2}, \dots, n_k^{m_k}$$

Where $$n_j, m_j \in \mathbb{Z}$$. We will transform this into a new sequence of length $$k+1$$ by adding a new term $$n_k^{m_k} + d$$, and multiplying each term by an integer $$C$$. So we have

$$C \cdot n_1^{m_1}, C \cdot n_2^{m_2}, \dots, C \cdot n_k^{m_k}, C\cdot (n_k^{m_k} + d) $$

This is now an arithmetic progression with difference $$C\cdot d$$ and we need to select $$C$$ such that each term is a perfect power. We can make the last term a perfect power by setting $$C = (n_k^{m_k} + d)^N$$ for some integer $$N$$. If we set $$N = m_1 \cdot m_2 \cdots m_k$$ then each of the proceeding terms will also be a perfect power, so the inductive step is complete.

[reveal]

Another arithmetic progression

Let $$D(n)$$ denote the sum of the digits of the integer $$n$$. For instance $$D(1234) = 1+2+3+4 = 10$$. Does there exist a (strictly) increasing arithmetic sequence with $$1000$$ terms, $$a_1, a_2,\dots, a_{1000}$$, such that $$D(a_1), D(a_2),\dots, D(a_{1000})$$ is also a (strictly) increasing arithmetic sequence?

Critical Line Volume 15 – Solution:

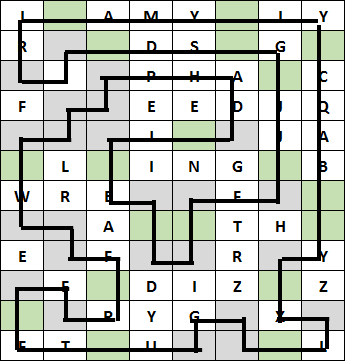
Leaving a solution: FEELING RATHER DIZZY

Very sorry for the mistake indicating 15 letters instead of 18 made up the solution. And congratulations to all who still solved and sent through correct submissions! The winner, through entry in what must be close to record time, is Stephen Edwards. Well done, Stephen.

CPD: Actuaries Institute Members can claim two CPD points for every hour of reading articles on Actuaries Digital.