The Critical Line – Volume 2

Welcome to the second instalment of the Critical Line!  The observant among you will notice that I am not Oliver, author of the first instalment. Writing duties of this column will be shared between a few different authors. Oliver’s previous column mentioned both a famous unsolved problem, and a sequencing problem.  In that spirit, I’d like to mention one of my favourite problems, the Collatz Conjecture.  Like many good maths problems it is very simple to understand what is being asked, but a fair bit harder to prove.

Collatz Conjecture

Start with any positive integer n.  If n is even, divide it by 2.  If n is odd, multiply it by 3 and add 1.  Repeat the process indefinitely.  The conjecture says that no matter what value of n you start with, you will always eventually reach 1.

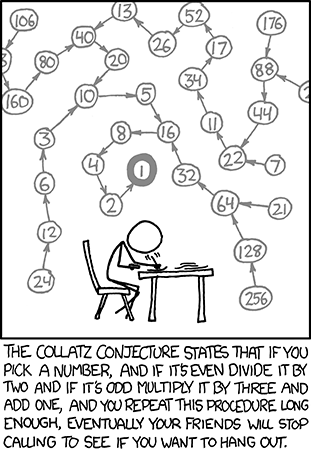
For example, start with n = 13.  The path will then be 13, 40, 20, 10, 5, 16, 8, 4, 2, 1 at which point the 4-2-1 will keep repeating.

If anyone sends me either (i) a valid original proof of the conjecture, or (ii) a counter-example that disproves the conjecture, I’ll double the Institute’s regular prize out of my own pocket and send you $100!

An alternative phrasing of the conjecture is provided by Randall Munro here:

An infinite deck of cards…

Now for a more reasonable problem.  In studying the mathematics of games, analytical shortcuts that give good approximations can often be had by using what is known as an infinite deck of cards.  By that we mean that when we draw a card, probabilities of outcomes don’t depend on what cards have already come. For a standard infinite deck, each value (Ace through King) always has a 1/13 chance of being drawn.

Blackjack is a great game for using this technique. Today’s problem concerns only the dealer’s hand.  The dealer will draw cards until their hand totals 17 or more.  Aces count as 11 if that makes the hand total 21 or less, and count as 1 otherwise.  (E.g. A-6 is 17, and 6-6-A is 13.)  Jacks, Queens and Kings count as 10, and all other cards (2 through 10) count as their face value.  Any hand value over 21 counts as a “bust”.

The six possible outcomes for the dealer are therefore 17, 18, 19, 20, 21 and Bust.

Analysing the likelihood of these six outcomes using an infinite deck is a problem well suited to actuarial techniques, and can be solved precisely rather elegantly (hint: Markov Chains).  These six probabilities can also be found on the internet fairly easily, so I’m going to add a small twist to the puzzle.

Part 1.  Remove all of the 5’s from the infinite deck (so that each remaining card value has a 1/12 chance of being drawn).  What are the probabilities of each of the six dealer outcomes? Answer exactly to six decimal places.

Part 2.  Reinstate the 5’s, and now remove all of the Kings.  Now what are the probabilities to six decimal places?

For your chance to win $50, send your solution to the Infinite Deck puzzle to ActuariesMag@actuaries.asn.au

CPD: Actuaries Institute Members can claim two CPD points for every hour of reading articles on Actuaries Digital.